日记
任重而道远啊。
建议降红。
也是终于在提示下做出来了。
我们发现正着做十分的难,考虑正难则反。我们管最后剩下的叫“原初”。设 dpi,j 表示在还剩 i 个人的情况下原初在 j 的概率。那么初始化就是 dp1,1=1,每个点的答案就是 dpn,i。
考虑如何转移。我们分类讨论:
- i=1
显然它会有两种情况:一种是前面的死了,从 dpi−1,j−1 转移来,一种是前面的活了,从 dpi,j−1 转移来。那么 dpi,j=2dpi−1,j−1+dpi,j−1。 - i=1
显然它也会有两种情况,但是其中一种是它死了,那么它就不可能成为原初,不用转移。剩下的就只有它活了这一种情况。dpi,j=2dpi,j。
然后就是喜闻乐见的手解 3000 元方程组了。我们可以设 dpi,1=x,然后再把 dpi,1 表示成 ax+b。解出 x 之后就可以转移了。
致敬传奇手模王。我手模死活模不过,把代码写出来过了?
我们发现一个 ai 会在区间 [l,r] 之内做出贡献当且仅当 ai−1 没在 [l,r] 内出现。于是我们对于每个 ai 分别计算贡献。我们设 L=ai−1上次出现的位置,R=ai−1下次出现的位置。那么 ai 就会对 l∈(L,i],r∈[i,R) 的区间造成贡献。
然后兴致勃勃的打代码测样例,发现过不了。究其原因是如果区间内有多个一样的 ai,只能计算一次贡献。我们只需要把 R 对 ai下次出现的位置 取 min 就行。
我们发现,如果要更改 hi,一定是把 hi 改的和 hi−1 一样。这样做的效果相当于删除了一个 hi。要我们在删 k 个数之后最小化 i=1∑nmax(0,hi−hi−1)。
我们设 dpi,j 表示 [1,i] 里保留了 j 个数。那么转移就是 dpi,j=min{dpk,j−1+max(0,hi−hk)}。复杂度 O(n3),可以通过。
我们设 dpi,j,k 表示从 1→i→n→i,第一次到 i 时有 j 的油,第二次到 i 有 k 的油。那么转移是:
⎩⎨⎧dpi−1,j,k→dpi,j,kdpi−1,j,k+pi→dpi,j+fi,kdpi−1,j,k+pi→dpi,j,k−fi这里不买第一次来时买第二次来时买注意 j+fi 要对 h 取 min,k−fi 要对 0 取 max。
我们设 dpi,j,k 表示已经匹配了前 i 维,离 p 的距离已经有 j,离 q 的距离已经有 k 的方案数。转移时枚举当前的位置 (r,r),dpi,j,k=∑dpi−1,j−∣pi−r∣,k−∣qi−r∣。我么发现,如果把能转移到 i,j 的 i′,j′ 画在平面直角坐标系中时,是一条 k=1 的直线 + 一条 k=−1 的线段 + 一条 k=1 的线段。
就像这样:
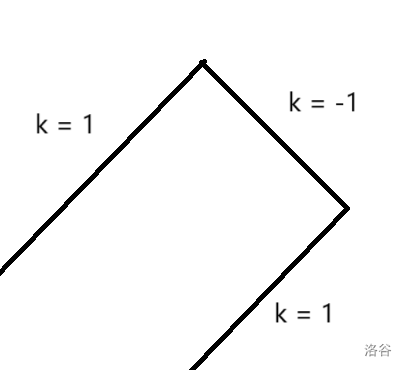
设 x=∣pi−qi∣,那么两个拐点的坐标分别是 (j−x,k),(j,k−x)。用一个 sum 维护一个 k=1 线段上的前缀和,pre 维护一个 k=−1 线段上的前缀和即可。枚举状态 O(nd2),转移 O(1),总复杂度 O(nd2)。
成功驯服 Godot,这周末开始做 BattleSweel。


