日记

码力得到史诗级增强。

堆 # Link to 堆

给定有 $n$ 个数的数组 $a$。有 $q$ 次询问，每次询问给定一个 $p$，要求进行 $n$ 次操作。初始有可重集 $S = \{a_i \mid i \in [1,p]\}$。第 $i$ 次操作的流程如下：

1. 取出 $S$ 里最大的数 $x$，让 $sum$ 加上 $(-1)^{i - 1} \cdot x$，将 $x$ 从 $S$ 里删除。
2. 如果 $p + i \le n$，将 $a_{p + i}$ 加入 $s$。

求每次询问过后请输出 $sum$ 的值。

我们先进行 $1$ 次 1 操作，那样操作顺序就反过来了。然后我们经过一番手模，发现这时 $x$ 是单调不增的，因为要是有 $a_{p + i} > x$ 就直接被取走了。我们可以每次操作用 $cnt$ 数组记录每个数的出现次数。维护一个 $max$ 指针，初始为 $n$。每次询问就直接去模拟：

• 加入的 $a_{p + i} < max$
  取出 $max$ 然后往下暴力找新的 $max$。
• 加入的 $a_{p + i} \ge max$
  直接取 $a_{p + i}$，$max$ 不变。

然后直接输出模拟出来的 $sum$，每次询问复杂度 $O(n)$，总复杂度 $O(nq)$。需要 现代硬件上的常数优化。

不让宋佳兴来讲卡常简直可惜了。

列队# Link to

我们发现行之间都是独立的，所以我们可以把整个矩阵分成这个样子：

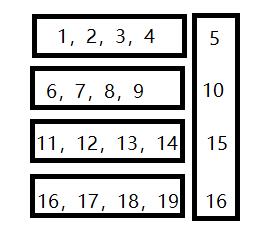
然后我们发现我们需要一个这样的数据结构：支持插入一个数，删除一个数。我们一看：平衡树！！但是太难写了，于是我们决定使用权值树状数组。先把所有的数都置为 $1$。每次删除的时候二分出来第 $k$ 个 $1$，将其置为 $0$ 就是了。然后有加入进来的外来数就用 vector 存下来就是了。

小明的树# Link to

我居然能在不看 std 的情况下自己打出来一个实现还算优秀的 AC 代码？

设第 $i$ 个点在 $a_i$ 时刻被点亮。

考虑如果是记美丽的时刻的个数如何做。我们发现一个时刻美丽当且仅当所有未点亮的灯泡形成一个连通块。而如何记连通块个数呢？设第 $i$ 个时刻时，连通块个数有 $X_i$ 个。我们发现连通块个数等于点数减边数。而在时刻 $i$ 有 $n - i$ 个未点亮的点。那么 $X_i = n - i - \text{两端都没点亮的边数}$。我们发现对于边 $(u,v)$，它会对 $i \in [1,\min(a_u,a_v))$ 的 $X_i$ 做出 $-1$ 的贡献。那么答案就是最小值的个数，可以用线段树维护。

但是我们的答案并不是记“美丽时刻的个数”。我们设 $Y_i$ 表示第 $i$ 时刻亮灯的灯泡的连通块个数。效仿 $X$，$Y_i = i - \text{两边都亮灯的边个数}$。那么显然，边 $(u,v)$ 会对 $i \in [\max(a_u,a_v),n)$ 的 $Y_i$ 造成贡献。

我们用线段树维护：$X_i$ 的最小值；$X_i$ 最小值的个数；$X_i$ 是最小值的位置的 $Y_i$ 的和。那么边的变化就是对 $X,Y$ 的区间加减。直接维护就行了。

后日谈 # Link to 后日谈

其实黑题也没那么难哈。