
5月每日总结
转眼就五月了啊,时间不多了。
5 月 3 日 Link to 5 月 3 日
值得记录的也就两题。
Neo’s Escape Link to
我们发现,一个克隆体一次会按掉一个区间内的所有按钮。那么就直接 dp。设 为把 这个区间内的所有按钮的都按完的最小克隆体数量。
转移十分的好写:,但是 一定要是一个克隆体能够全按完的。可以证明 能被一次性按完,当且仅当 形如:。
这么看,似乎连 暴力都不好写的,但是我们拥有 DS 之力,我们可以维护 满足 这段区间单调不降,再维护一个 满足 这段区间单调不增。感性理解: 一定是单调不降的,于是我们的 肯定最小越好。我们发现对于每个 , 的每个子区间肯定都是合法的,那么 转移的最优决策点肯定都不会在 右边。我们直接用线段树维护区间取 ,单点查询。
Censoring G Link to
既然出现在了 AC 自动机的题单里,我们肯定就要用 AC 自动机嘛。
对于文本串的匹配,我们用一个栈记录一路走来的 ,和 记录答案。如果匹配到的这个点,是一个模式串 的结尾,栈和 都 pop 次。然后 变成新的栈顶,继续匹配。
后日谈 Link to 后日谈
正式因为配不上她,所以我才在努力变强啊。
有奖竞猜:“她”代指谁?
5 月 4 日 Link to 5 月 4 日
时间不多了。
T1 Link to T1
明天再问问。
一定记得哦!
T2 Link to T2
AC 自动机 dp。
我们设 表示匹配前 个字符的方案数。我们在 AC 自动机上走到的 ,我们暴力跳 ,如果跳到哪个节点是一个模式串的结尾,那么就说明该转移了。设这个模式串的长度为 ,那么显然的转移是 加上 。
考虑如何优化。因为只有模式串的结尾的那几个节点对转移有用。我们对于每个节点记录一个 表示跳 能跳到的第一个节点使得它是某个模式串的结尾。每次直接跳 就行。时间复杂度 。
T3 Link to T3
原题。但是需要一些奇技淫巧。
分两种情况考虑。
如果有集合的交集是 ,那么肯定只有一个。因为如果有多个,那么肯定可以合并。那么我们把所有的线段按照长度从大到小排序,取前 的就行。
那有人要问了:如果剩下的有交集怎么办?没事,dp 会出手。
剩下的是没有交集为 的情况。
我们把所有的线段按照左端点排序。但是我们发现,排序完了依然不好做。究其原因是有线段包含了别的线段。我们考虑这些“包含了别的线段的线段”。如果它和它所包含的线段出现在了一个集合内,那么肯定不会影响到这个集合的答案。反之它肯定是单独成一个集合。因为如果它和别的线段一起,只可能使答案减少。
我们把“包含了别的线段的线段”的踢出去,那么剩下的肯定是左右端点都单调递增的线段。由于这样我们取一个集合只会取一个区间,于是我们 dp:设 为前 个集合用了 条线段。转移就是枚举 当作最后的一个集合,然后转移。前缀和优化。
但是我们发现这玩意是 的,无法通过。考虑 奇技淫巧。如果 ,也就是 跑不过,我们就不跑 dp,跑完上面的贪心就输出。能过就对了。
T4 Link to T4
没改。
文本生成器 Link to
正难则反。
考虑如何求不可读的方案数。建出 AC 自动机,然后对于每个节点记录一个 表示它或者它在 树上的祖先是否有某个是一个模式串的结尾。然后 表示当前已经有了 个字符,在 节点上。枚举 在字典树上的每个儿子 ,如果 的 不为 ,那么就可以转移,否则不行。答案就是 。
Video Game G Link to
我连最基础的 dp 都做不出来了?完蛋了
设 表示已经匹配了 个字符,当前在 节点上。对于每个节点记录一个 表示这个节点是几个模式串的结尾。如果我想转移到 ,那么我们就得从 往上跳 ,记录从 路径上的所有点的 之和为 ,转移就是 对众多 取 。可以优化。
后日谈 Link to 后日谈
唯有自救。
5 月 6 日 Link to 5 月 6 日
昨天晚上打 CF 去了,没写日记。
Needle in a Numstack Link to
码力题。码力太强导致赛时没写出来。
Spruce Dispute Link to
考虑如果已经删完点了如何求出最大的答案。我们考虑一个点 。设它的子树大小是 ,那么它的贡献就是 。为了最优,我们会让每一条路径都经过重心。因为重心的每个子节点 所对应的子树大小 不会大于 。于是顺理成章的把重心当成根,无根树就变成了有根树,总的答案就是每个点到根的距离之和。
但是这道题恶心的很,还要我们构造方案。我们发现构造方案主要是要满足重心的每一颗子树内没有颜色相同点,我们可以把 的颜色设成 ,因为一颗子树的大小不会超过 。
考虑删点。我们发现删掉一个点的代价是 ,因为自己没贡献了,然后子树内的每个点深度还减了 。经过一番推导,我们发现最优的点一定是深度最小的叶子节点。删了然后按照上面的方法构造即可。
Lost and Pound Link to
我们设 表示还有 轮,还要按 次胜利按钮的获胜概率,初始为 。
我们发现,每次按完之后都会重新打乱,也就是说不存在知道获胜按钮的情况。于是我们就可以抛弃顺序,直接转移。设按了 个按钮,每个按钮按了 次,因为没有顺序,我们钦定 单增。有转移:
分别表示获胜按钮被按到了 次或者压根没按到。
我们发现 十分的小啊,可以直接枚举所有的 。大概有 多个。加上枚举状态 ,时间复杂度 。
Removal of Multiples Link to
发现答案最多不会超过 ,剩下的就是权值线段树的事了。
记得加上奇技淫巧小剪枝。
Ancestor Relation Link to
写日记的时候才发现昨天做了好多题。
想想怎么判无解。题目里说 时, 在一条从上往下的链上。而 ,作为根,肯定和所有的点都在一条链上。如果不是,就说明无解。还有:我们看,如果有 ,那么就说明 和 相对别的点的位置相同,可以得到他们在一条链上,也就是说必须有 ,否则就无解。还有,如果有 ,那么就说明 是 的祖先,如果没有 ,同样无解。
剩下的就全是有解的状态了。考虑两个点何时能够交换。发现当且仅当 时能够交换。我们就可以把 个点分成几个集合, 相同的在一个集合。每个集合的方案数就是 ,乘起来即可。
我们发现所有的操作都可以用 bitset 维护。所以时间复杂度 ,其中 是 bitset 常数。
Apple Tree Traversing Link to
码力依然强大。
我们发现“字典序最大”,而排在前面的又是长度,我们肯定是让长度最大。于是我们先取个直径。取完直径之后就分成了几个子树,递归处理即可,时间复杂度 。
Cycling (Easy Version) Link to
我们设 表示跳到了 后面还要多少代价才能跳到最前。初始有 。转移时考虑最后一个区间 。我们发现最优策略是把 里的最小值拿过来一直超,代价为 ,分别表示把最小值掏过来,最小值跟着走,超最小值的总代价。于是我们拥有 dp,可以通过简单版。
Cycling (Hard Version) Link to
不会 做法。
我们发现其实我们是可以确定区间的分界点的。比如我们拿一个样例:4 1 3 2。我们首先拿 一直超。直到我们发现这里出现了一个 。我们发现拿 一直超比拿 一直超更优。于是我们改拿 一直超。我们把 的意义改一下,改成:先拿最后的一直超,直到现在超的比前一个数小,我们改拿前一个数继续超,如此循环往复。用此策略超到最前面的最小代价。显然,这玩意可以 预处理。
不懂策略的看过来
比如4 1 3 2 5 3,先拿 一直超,直到我们看到了 ,就改拿 继续超,然后我们又看到了 ,我们又改超 。
那有人要问了:你没考虑把一段区间的最小值掏过来然后拿它一直超的情况啊?确实没考虑,所以我们现在考虑。依然是这个样例:4 1 3 2 5 3。假设我们现在在第 个数后面。如果我们想把 掏过来超,那么需要花费的代价是 。每一项分别表示:已经走到 所在的位置还需要的代价, 往返需要的代价,不停的超过 需要的代价。
我们再推几组样例,会发现:如果我想把 拿到 的位置然后一直超,所需要的代价是 。这玩意可以看做是一个关于 的一次函数。总共 个一次函数。我们把所有的一次函数都塞到一颗李超线段树里,然后每个位置的答案就是在这个位置查最小值。
05-04 T1 Link to 05-04 T1
我居然记得去问?
首先有一个结论:如果上一层有 个非叶子节点,上上层有 个,那么这一层至多有 个非叶子节点。因为每个点可以选择是当左儿子还是右儿子,分别代表上一层和上上层。
我们肯定是按照 从大到小,深度从小到大填的。设 表示当前的深度为 (这一层的叶子已经确定),一共有 个点被钦定成了叶子,这一层还有 个空位,下一层还有 个空位。转移枚举下一层钦定 个作为叶子:
我们发现 其实是不必要的,状态改成 。依然是钦定这一层有 个叶子:
之所以加的值从 变成了 ,是因为最开始钦定所有的深度都为 ,转移时使一段后缀的深度 。
我们发现这依然是 的,跑不过。究其原因是转移是 的。考虑简化转移:
- 再钦定一个点作为叶子:。
- 往下一层:。
于是转移就变成了 ,总复杂度 。记得滚动数组优化空间。
关于
因为本来就钦定的剩下的都在这一层,所以转移的时候不用加。 都 的原因是这一层少了一个, 自然要 。但是上一层又没变,所以 也减了 。
后日谈 Link to 后日谈
才发现我这两天做了这么多题。
因为每次想要颓废的时候看到草神,就感觉颓废对不起自己,于是再切一道题。
拼命练就的本领绝不会辜负自己。
5 月 7 日 Link to 5 月 7 日
你怎么敢在草神面前睡觉的???!!!
还好还骗了 分,不然今天就挂了。
T1 Link to T1
大模拟。
分做法:
暴力枚举,时间复杂度 。
分做法:
发现只有有重叠的情况才需要特殊考虑。而这种情况又只有 个,我们枚举这 种特殊情况就行,复杂度 。
T2 Link to T2
感性理解:交换的 一定是 且 的。我们设在 区间内,大于 的数有 个,小于 的数有 个, 同理。那么交换 会使逆序对数量减少 。移一下项变成 。我们发现这玩意就是区间 且 的个数乘 。
我们把每个点塞到平面直角坐标系上面。第 个额点的坐标是 。那么上面的柿子就相当于:取一个左上角的点和一个右下角的点,它们框出来的矩形的里的点的数量(不包括边界)。使用扫描线维护。
如何使用扫描线维护?我们首先发现一个性质:如果有 且 ,那么显然 比 优, 就不会成为“左上角的点”。言外之意:只有 , 才可能成为最优解里的“左上角的点”。同理可得,只有当 时才可能成为“右下角”的点。我们把这些点分类:不能成为边界点的叫贡献点。考虑从左往右扫描:
- 遇到一个贡献点
我们维护一个 表示当前的这个点能对值在 区间内的“左上角的点” ,于是我们直接权值线段树区间加 。 - 遇到一个“左上角的点”
更新 即可。 - 遇到“右下角的点”。
我们对于每个贡献点都记录一个 表示它对 区间内的作了贡献。由于我们维护的“右下角的点”也该是单增的,这个点下面的贡献点都不会有贡献,所以我们就把 的每个 区间减 (此时 还没有更新),然后更新 ,并统计答案。当前的答案就是全局最大值。
T3 & T4 Link to T3 & T4
不睡觉也做不出来。
后日谈 Link to 后日谈
睡觉的原因是昨天晚上睡不着,导致早上困死。
以后不准睡了哦!
5 月 8 日 Link to 5 月 8 日
任重而道远啊。
Tournament Link to
建议降红。
Bomb Game 2 Link to
也是终于在提示下做出来了。
我们发现正着做十分的难,考虑正难则反。我们管最后剩下的叫“原初”。设 表示在还剩 个人的情况下原初在 的概率。那么初始化就是 ,每个点的答案就是 。
考虑如何转移。我们分类讨论:
显然它会有两种情况:一种是前面的死了,从 转移来,一种是前面的活了,从 转移来。那么 。
显然它也会有两种情况,但是其中一种是它死了,那么它就不可能成为原初,不用转移。剩下的就只有它活了这一种情况。。
然后就是喜闻乐见的手解 元方程组了。我们可以设 ,然后再把 表示成 。解出 之后就可以转移了。
Double Sum 3 Link to
致敬传奇手模王。我手模死活模不过,把代码写出来过了?
我们发现一个 会在区间 之内做出贡献当且仅当 没在 内出现。于是我们对于每个 分别计算贡献。我们设 。那么 就会对 的区间造成贡献。
然后兴致勃勃的打代码测样例,发现过不了。究其原因是如果区间内有多个一样的 ,只能计算一次贡献。我们只需要把 对 取 就行。
Laminate Link to
我们发现,如果要更改 ,一定是把 改的和 一样。这样做的效果相当于删除了一个 。要我们在删 个数之后最小化 。
我们设 表示 里保留了 个数。那么转移就是 。复杂度 ,可以通过。
Fuel Round Trip Link to
我们设 表示从 ,第一次到 时有 的油,第二次到 有 的油。那么转移是:
注意 要对 取 , 要对 取 。
Manhattan Cafe Link to
我们设 表示已经匹配了前 维,离 的距离已经有 ,离 的距离已经有 的方案数。转移时枚举当前的位置 ,。我么发现,如果把能转移到 的 画在平面直角坐标系中时,是一条 的直线 + 一条 的线段 + 一条 的线段。
就像这样:
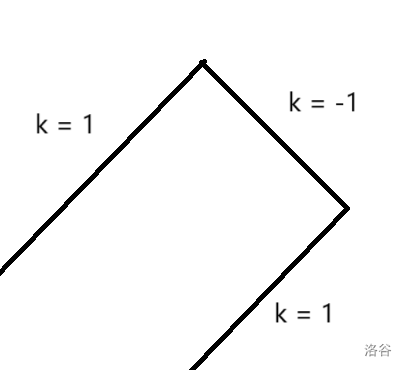
设 ,那么两个拐点的坐标分别是 。用一个 维护一个 线段上的前缀和, 维护一个 线段上的前缀和即可。枚举状态 ,转移 ,总复杂度 。
后日谈 Link to 后日谈
成功驯服 Godot,这周末开始做 BattleSweel。
5 月 9 日 Link to 5 月 9 日
神奇模拟赛。
T1 Link to T1
主席树板子。
还好对拍了,不然就废了。
T2 Link to T2
我们把 打包成一个 pii。然后把它塞进 这个队列里。队列里按照 排序。我们发现,如果有两个 ,把它打包成一个更大的 肯定更优。如果说 分成两半还有剩的,就取一个剩下的高度最大的填进去,这样是最优的。
最后计算 的答案就行。
T3 Link to T3
神秘小数论,尝试驯服但是被反噬了。
T4 Link to T4
神秘小图论。
后日谈 Link to 后日谈
今天因为没人讲题导致颓废了一下午。究其原因还是自己太菜看不懂题解。
期待明天的重大半日游CCPC。
5 月 12 日 Link to 5 月 12 日
我们拥有最强大的码力和最靠谱的队友。
我的俩队友一道题都没做出来。。。
列车 Link to
我们把线段的两个端点们离散化。然后每个整的区间就被切成了许多小区间。对于一个区间,他的每个子区间都要加上 。然后最后的答案就是所有子区间的最小值。
这个 子区间 卡了我一天。
黄金替罪羊 Link to
我们发现,每个 的取值是会影响后面的,也就是说它有后效性。不能搞普通的 dp。
我们钦定在 过去的自己 开始行动的时候自己的位置在 ,枚举每个 。设 表示 过去的自己 走了前 步,自己走了 步,过去的自己 位移为 ,自己的位移是 的方案数。
考虑转移:
- ,可以从 转移而来。
- ,可以从 转移而来。
- ,可以从 转移而来。
- ,可以从 转移而来。
- 在 时不转移,,因为自己黑化了,不合法。
注意这个 和 是同时变化的。就比如如果同时满足条件 ,就可以从 转移来。对于每个 ,答案就是 (就是枚举自己最后的位置),最终的答案就是把每个 的答案加起来。
我们发现 , 就小于 ,坐标区间的长度就是 ,而对于我们的 状态和一个 的枚举 ,总共 的复杂度,肯定是跑不过的。我们需要优化。
我们发现,在第 步是,还能做的位移至多为 ,而还要做的位移就是 ,如果有 ,就肯定不可行,直接 continue。
时间复杂度还是 ,但是现在跑的过了。
Quartet Swapping Link to
我们发现交换的时候不会改变位置的奇偶性。比如有个数在 ,再怎么换也换不到 或者 去,只能在 为奇数的位置上动。于是我们盲猜一个结论:把奇数位置上的数和偶数位置上的数排序后输出。成功的吃到一发罚时。
我们又发现一个性质:交换的时候,逆序对的变化是 。也就是说,逆序对数量的奇偶性也不会发生变化。于是我们把原序列的逆序对数量算出来,排序后的数量算出来。如果奇偶性相同就直接输出,反之把排序后数组的第 项交换一下,因为这样既能改变奇偶性又能使字典序次小。
后日谈 Link to 后日谈
总结了一下,感觉这次 CCPC 还是收获颇丰。
拼命练就的本领绝不会辜负自己
5 月 13 日 Link to 5 月 13 日
传奇耐骗王。
T1 Link to T1
把 异或上 ,再把 按照异或差分。(就是说 )这样一个区间 翻转就变成了取反 。我们把 建边。那样就分成了许多连通块。每个连通块之间的情况数是独立的。
对于每个连通块单独考虑。我们掏一个生成树出来,那么我们一定只用翻转树边就行了。对于每种生成树,方案都是固定的。于是一个连通块的方案数就是这个连通块的生成树数量。为 。
如何构造答案呢?我们从叶子开始。dfs 时记录一个 表示从哪条边走到的 。因为我们是从叶子往上生成方案的,所以翻转 不影响下面的点。于是直接判断 是否为 ,是就翻转 和 的 ,并构造答案。
T2 Link to T2
我们发现,每个 会对 个数造成贡献。也就是说 数组的总和 是 数组的总和 的 。这样我们就能求出 。
接下来我们考虑如何求 第 行的和 。我们发现,如果把 的第 行的数加起来,就相当于把 的第 行算了 次,再把 除了第 行的加起来。也就是说:
解出来发现 。如法炮制求出 。又有 ,就可以解出 了。
T3 Link to T3
赛时都想得到,这里就不说了。
码力该比思维好练吧?
一个 manacher 卡我一晚上。
T4 Link to T4
神秘小随机化。明天再问问随机化大佬。
后日谈 Link to 后日谈
原来 NOIp 只有 也可以进队啊?
5 月 14 日 Link to 5 月 14 日
今天是民国 114 年 5 月 14 日。
SuperGCD Link to
纯恶心人的题。谁用 C++ 写谁有病。
Fox And Jumping Link to
口胡一下发现当且仅当选出来的 的 为 的时候才会是可行的。于是我们直接设 表示把 干成 的最小代价。转移就是 。用 map 存下来就行。
Boxes Link to
我们首先把 都除以一个 把他们变得互质。 能通过这种操作变得某个为 当且仅当这时的 。证明如下:
充分性:进行一次操作后,无论较小值是谁, 在二进制下的后缀 个数都是增加的,这样最终就会变成 。
必要性:手玩一下样例。
于是就是喜闻乐见的打代码时间了。
Binomial coefficients Link to
根据常识,我们发现 的 不会大于 ,于是我们直接枚举 ,因为在 不变的情况下 随 单增,我们直接二分 然后统计答案。
记得排序和去重。
荒岛野人 Link to
野人的事情让野人自己想去
我们发现这玩意长得跟个粑粑同余方程似的,于是直接枚举 ,再枚举 两个野人,exgcd 解出最小的 ,如果 小于等于 ,就说明他们会打架,否则就可行。
后日谈 Link to 后日谈
明日目标:。
5 月 15 日 Link to 5 月 15 日
达成目标。
T1 Link to T1
发现如果以 个为一组,那么这组内的方案是固定的。于是先处理最底层的,然后再处理 轮之后的。
T2 Link to T2
神秘小 bfs。直接搜。
后日谈 Link to 后日谈
现在似乎又变的颓废了,这可不行啊。
5 月 18 日 Link to 5 月 18 日
这就是你所追求的 智慧 ?
Crazy Atek Link to
我们发现,如果一个数满足数位和和数位积相同,那么他们就一定会有许多 。考虑如果对于一个数 ,它的数位和是 ,数位积是 ,那么它就需要再加 个 就能变得数位和等于数位积。因为加一个 ,会使数位和 ,但是数位积是没变化的。
我们先把 扔掉,只用 的数字。把每个 的数字搭配都搜出来。只有大约 个。然后我们就可以通过这些数算出它还需要的 的个数,并算出这些数字组合能凑出多少种不同的数。把他们按照添 过后的总位数排序,每次查询的时候二分一下就行。
Clown Fiesta Link to
根据欧拉定理,有 。接下来就是喜闻乐见的推柿子时间。
有 。往上套就行。当然,如果哪个 了,就不用继续了,因为怎么模都是 了。
后日谈 Link to 后日谈
周六的 CF 十分的简单啊,但是我没打。不然又可以加大大的 rating
然而在我打 abc 的时候,一个傻逼加了我的好友,妄图骗走我的 steam 号。直接拉黑删除举报。
5 月 19 号 Link to 5 月 19 号
窝补药补政治历史啊啊啊
一坐到教室里就想到 11 月 NOIp 过后我就得回来学 whk 啊啊啊啊啊。
窝补药学文化课啊
GCD Link to
考虑枚举 的每个因数。设枚举到的因数是 (),设 。因为我们要让 ,所以 必须得和 互质,那么就是说有 个 使得 ,直接 加上 。
最大公约数之和 Link to
和上一题一样的,不过没有 这个条件, 加上的值变成 。
搭配飞行员 Link to
我们把每个正驾驶与源点连边,流量是 ,每个副驾驶和汇点连边,流量 ,可以搭配的正驾驶和副驾驶连边,流量 。能够凑出的最大对数就是最大流。
如何构造方案呢?我们考虑一条逆向边,如果它有剩余容量,就说明正向边被选了,输出就好。
餐巾计划 Link to
把一天分成两个点,一个早上,一个晚上。
- 每天早上连一条边到玩上,容量 ,费用 ,表示可以把脏的从早上留到晚上。
- 从汇点连一条边到每天早上,容量 ,费用 ,表示每天早上可以买干净的。
- 对于一个洗洁部门,设它 天洗完,费用 ,从第 天晚上到 早上建边。容量 ,费用 ,表示可以把脏的拿去洗。
- 每天早上往汇点建边,容量 ,费用 ,表示第 天早上要有 条干净的。
- 源点往每天晚上建边,容量 ,费用 ,表示第 天网上会多 条脏的。
然后就是喜闻乐见的最小费用最大流时间了。
后日谈 Link to 后日谈
窝补药学文化课啊
你现在什么也改变不了,你需要变强。
5 月 20 日 Link to 5 月 20 日
终于上完政治和历史课了。
课上:生命因何而沉睡?因为我们连着上了 节政治课。
太空飞行计划 Link to
我们把每个实验当作一个点权为 的点,从源点往它建边,容量为 ,把每个仪器当作点权为 的点。从它向汇点建边。容量为 。对于每个实验,从它到它所需的仪器建容量为 的边。那么对于每个实验,选了它就表示源点到它的边满流。对于每个仪器,选了它就表示它到汇点的边没有流量。于是我们就相当于求一个割,它的值为 ,而总的利润是 ,那么我们要求的就是最小割也就是最大流。
最小路径覆盖 Link to
我们先把每个点都当作一条路径,那么我们就去考虑合并路径。如何合并呢?设第一条路径的结尾是 ,第二条路径结尾是 ,当且仅当 有边的时候才能合并。我们把每个点 拆成两个点:出点 和入点 。对于输入的每条边 ,从 建边,容量为 。再从源点向每个出点建一条容量为 的点,从每个入点向汇点建一条容量为 的点。这显然是一个二分图。对于其中的一个长度为奇数的匹配路径,它一定是由 再从 最后再从 的。对于每个 ,相当于新合并了两条路径。对于每个 ,它相当于取消了两条合并。因为是奇数,所以 的数量肯定是比 的多一条。而一个匹配路径,就相当与网络流上的一条增广路。于是我们求出最大流之后用 减掉它就行。
魔术球 Link to
二分一个 出来。把每个 且 是完全平方数的建一条边,求出这个图的最小路径覆盖。如果大于 就 ,反之 。
方格取数 Link to
我们按照 的奇偶性给每个点分类。 的为白色,其余的是黑色。那么从白色点往四联通的黑色点建边,容量 ,从源点向白色点建边,从黑色点向汇点建边,容量都是 ,那么答案就是所有点的权值和 - 最小割的值。
运输问题和运输问题 Link to 和
最小费用最大流板子。
后日谈 Link to 后日谈
还是紅蓮華好听啊。
5 月 21 日 Link to 5 月 21 日
为什么不写??!
T1 Link to T1
不知道暴力为啥错了,反正 分,不管他了。
T2 Link to T2
我们发现代价式子里有个绝对值:,考虑把 排序后变成 ,那么代价就变成了 。
再把贡献式子转换一下:。我们发现要让 尽量小,于是把 从大到小排序,把 从小到大排序,然后让 就行了。
T3 Link to T3
神秘小 dp。
我们发现,在左端点固定的情况下,右端点肯定是越大越优。于是我们设 表示在第 轮,左端点为 时右端点最大在哪里。
考虑转移:
- 取了个前缀:,条件:。用一个前缀和优化。
- 取了个后缀:,条件 。转移的时候记录一个变量就行。
时间复杂度 ,常数有点大。
T4 Link to T4
你说你都想到了为啥不写呢?
后日谈 Link to 后日谈
下午不想改 C 于是打算去做网络流。但是网络流 好像做不出来于是找了两道网络流水题做。做了半天发现太简单了,于是又回去做网络流 题。
我发现我不缺知识也不缺思维。我甚至想得到别人想不到的东西。但是我缺自信啊!我想到了也不敢写,究其原因时码力实在是太强了。我写出来的代码:在大量的 bug 中发现少量代码。一个树剖都能硬控我一上午。
还是得练码力啊。
5 月 22 日 Link to 5 月 22 日
还好昨天晚上没有写日记。
事情起因是这样的:我的电脑开机就蓝屏。它已经这么蓝屏过几次了,于是我决定修一下。他的错误代码是 MEMORY_MANAGEMENT。因为我的内存是不同频率混着插的,所以我早就料到它会出问题。于是我把机箱打开,想把不同频的两根条子拆下来。但是我的显卡把内存条挡住了,于是我又把显卡拆下来。但是装回去的时候,显卡没插稳。于是我被显卡硬控了 分钟。
其实上面的都算好的了。等我把电脑打开,我又发现有个人妄图加我的 steam 好友。我于是接受了。然而他又是一个骗子。超市他的马。
试题库 Link to
其实这玩意是个挺基础的建模了。
把每个类型连到源点上,容量是所需的题数,把每道题连到汇点上,容量是 。再把每个类型对应的题目连到这个类型上,容量也是 。那么能取到的最大题数就是最大流。如果最大流小于等于所需的总题数,就说明非法。
如何构造方案?我们发现,如果对于一个类型到题目的边有流量,就说明这个类型选了这个题目。
骑士共存 Link to
我们发现: 的奇偶性跳一下一定是会变化的,那么这题就和方格取数一模一样了。
最长递增子序列 Link to
我们先 dp 出以 结尾的最长不降子序列长度。这样第一问就解决了。
对于 的点,从源点往他建边,容量为 。对于 最大的那几个 ,从它建边到汇点,容量也为 。跑一个最大流,这样第二问也解决了。
我们再把 的容量设成 ,如果 最大的话把 的容量也设成 ,这样第三问也解决了。
数字梯形 Link to
网络流常用技巧:拆点。把一个点拆成两个点,一个入点和出点。每个点的入点向出点连边,容量是题目这个点的允许访问次数,代价是点权。一个输入的边 ,让 的出点往 的入点连边,容量是这个边的允许访问次数,代价是边权。
深海机器人 Link to
最大费用最大流板子,但是题意实在是晦涩难懂。
航空路线 Link to
其实也挺板的,参照数字梯形下面给的网络流常用技巧。
火星探险 Link to
其实你会发现,我基本已经会基本的网络流建模了。但是我的码力还是太强了,被一道题硬控一晚上。
后日谈 Link to 后日谈
我真的诗人吗?我的码力为啥这么强?到底怎么才能练码力啊??
今天不仅码力不行,还有 的冷空调给的 debuff,给我吹出肠胃病来了,今天一整天都是萎靡不振。
5 月 23 日 Link to 5 月 23 日
为啥会背疼啊?
Final C Link to
设 表示已经选了 根弦,第 根弦在二进制下又 位是 的方案数。初始化 ,转移就是 。最终答案就是 。
就是没想到最终答案。
Alex Combines Link to
我们发现对于每个区间,左端点也不是定的,右端点也不是定的。这十分的麻烦。考虑固定一个左端点或者右端点来考虑。
设 表示 这段区间是合法的。显然这玩意可以 预处理。查询的时候暴力一点:如果 , 就跳到 , 加 。注意 初始为 。
看到这一就应该自然而然的想到倍增了。
最长 k 可重区间集 Link to
建边就这样建:先离散化, 建一条容量 ,费用 的边,对于每个区间, 建一条容量 ,费用 的边, 建一条边,容量 ,费用 , 建一条容量 ,费用 的边,跑最大流就是了。
如何理解?我们发现如果有 条边重合了,那么一定需要至少 的流量。
星际转移 Link to
枚举时间,在时间和下一站之间建边。
后日谈 Link to 后日谈
今天还没消掉 空调给的 debuff。。。
5 月 26 日 Link to 5 月 26 日
这 gbc 看的我有点 emo 怎么个事?
GCD - Extreme (II) Link to
我们发现他让我们求这个东西:,显然可以转化一下:
到这个时候已经可以 做了,但是我们发现 , 的复杂度显然过不了。我们发现:一车 都是一样的。于是我们直接数论分块。复杂度直接降到 。
GCD Link to
也像上面一样,枚举每个质数,然后变成 的形式。
报数 Link to
我们发现:,套个 也能过。于是直接 筛就行。
Trailing Loves (or L’oeufs?) Link to
我都能做出来的题肯定是不用说了。
后日谈 Link to 后日谈
今天做数论做疯了。
溜冰溜爽了。给我看的差点哭出来怎么个事?
照理来说这里是日记,应该写点感想,但是我写日记的时候忘了当时的感觉了,于是不写了。再听一遍《熙熙攘攘,我们的城市》就下。
5 月 27 日 Link to 5 月 27 日
今天正经做的题只有两题,也是十分的颓废。
Fansblog Link to
我们预处理 的每个质数,那么判断质数的复杂度就会降一点。于是我们直接从 往下枚举 。题目让我们求 。根据威尔逊定理:。而 ,转换一下就是:
而我们都能直接枚举 了,直接枚举 也不是不行,求个逆元就是了。
出圈游戏 Link to
硬控我一晚上,如何呢?
我们发现,设当前这是被删的第 个人,那么 ,其中 表示这个被删的人和上一个的距离。
直接 exCRT 就是了。然而我的 exCRT 是一点问题都没有,被输入和算距离硬控了我也是个人物。
后日谈 Link to 后日谈
没啥谈的。我的冰溜完了,我要去找一部新番看。
算了还是再溜一遍冰吧。
5 月 28 日 Link to 5 月 28 日
神金研学,我不说。
反素数 Link to
我们发现 可以分解成这个样子:。
为啥是 ?
因为小于等于 的质数乘起来就已经 了。
我们还发现一个重要性质: 单调递增。
因为如果有 而又有 ,那么我们一定可以交换 ,得到更小的数却拥有一样的因数个数。
直接打表出来。
屠龙勇士 Link to
显然有杀每条龙的剑都是固定的,可以先通过模拟求出来。设杀第 条龙的时候剑的攻击力是 ,那么就有一堆同余方程组:
考虑如何解。显然普通的 exCRT 是不行了。
设前 个方程组的可以合并成 ,那么有:
可以化成这种形式:
exgcd 解就是了。
后日谈 Link to 后日谈
今天外套还被偷了。里面还有我的耳机。
也是对生活 充满了希望。
这还是我头一次在打 OI 的时候说的:今天怎么才周三啊!
也许最近的破事确实有点多吧,又是遇到了俩骗子,又是丢外套,又是生病,又是分流。。。实在是有点烦躁。我的脾气也变得火爆了。
小草神呢?小草神救一下啊!!!
别管了。今天先啥都别想了,睡觉吧。
5 月 29 日 Link to 5 月 29 日
我真的拥有思维吗?
Connecting the Graph Link to
想到 然后成功的被自己带偏了。
我们发现,如果没有那些乱七八糟的新边,肯定是把 数组排序之后依次建边来的最优。于是我们先把这些边加进去,边权就是 。再把新的边加进去,边权为 。最后跑 Kruskal 就是了。
这个故事告诉我们:最小生成树多半是要扯到 Kruskal 和 Prim 这俩上面的。
Disproportionate Tree Link to
直觉告诉我这个题要从叶子节点往上处理。
说明在竞赛里,直觉还是很重要的。
我一开始以为两个一样的数连的边不会有贡献,然后就朝着这个方向想了。深度从小到大处理,如果需要这个点造成 的贡献就把整颗子树都加上 。
理想很丰满,现实很骨感。我发现两个一样的点也会造成 的贡献。不过无伤大雅。先把 减掉 就是了,造成的贡献也从 变成了 。设当前在处理点 ,每次找到一个最大的 ,使得 ,把 减掉 , 的整颗子树加上 就行了。子树加可以用差分实现。因为线段树太长了
Driveaway Link to
我们考虑如何从 推到 。我们发现 时选的点集一定是 时的真子集。因为如果不是,那么一定有一个点,在 的时候被选但是在 是没被选。此时我们一定可以在 时选它使得更优。于是这么做就是了。我们把选走的都删掉,用链表维护。用一个大根堆堆维护选链表里的每对数造成的负贡献。选走一对数就把他的贡献从堆里删除。
后日谈 Link to 后日谈
我拥有思维吗?也许吧。
我拥有直觉吗?也许吧。
我拥有码力吗?这喷不了这是真没有
5月每日总结
© 伊埃斯 | CC BY-NC-SA 4.0
