伊埃斯的小站

树分治学习笔记

Mon Feb 17 2025
24 分钟
tech 学习笔记
3224 字

好久都没写学习笔记了。

吐槽：代码太长，洛谷国际站又爆炸了，没法用云剪贴板。

引入#

我们先来看看序列分治。序列分治通常是把一个大问题分成许多个小问题，最后合并就成了总的问题的答案。而树分治也是如此。

这里主要讲点分治和点分树，边分治不讲。因为不会

例题#

P3806 【模板】点分治 1#

点分治通常用于处理路径问题。比如这道题里的“有没有距离为 kk 的点对”其实就是“有没有长度为 kk 的路径”。

我们先将询问离线，随便认定一个点为根。那么路径有 22 种：经过根的和不经过根的。不经过根的可以递归的处理子树进行分治。我们只考虑经过根的路径。我们可以进行一次 dfs，处理子树内每个点到根节点的距离，和它属于哪个子树。然后按照距离给每个点排序，循环每一个询问 qryiqry_i，双指针找出没有长度为 qryiqry_i 且不属于同一个子树的点对。有就把 ansians_i 置为 11 并 break。没有就继续。

这样我们就成功的搞出了一个看似天衣无缝的做法。但是我们发现，当树变成链的时候，这个算法会退化到 O(n2)O(n^2)。究其原因是处理每个点所在的子树的时候，子树大小都是 O(n)O(n) 的。而总共有 nn 个点，那么和起来就是 O(n2)O(n^2)。

我们回到序列分治来找优化方法。我们发现，序列分治的分治中心一般是区间中点，因为满足这个性质：分出来的最大块最小，也就是最平均。因为分治的时间复杂度是 层数×O(n)\text{层数} \times O(n) 的。这样能使层数最小，从而使得时间复杂度最小。我们希望我们的点分治也能够这个样子。

我们发现，如果要使分的块（子树）最平均，我们想到重心当分治中心。每次找到重心作为根，这样就最平均了。那有人要问了：子树的重心不是当前节点的儿子的怎么办？因为我们会递归处理每个子树，当前块内的每条路径都会在当前或者递归后被处理。我们就把每次分治的中心设为重心，最大递归层数 log⁡2n\log_2 n。总时间复杂度 O(nlog⁡2n)O(n\log_2 n)。

code:

CPP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include<bits/extc++.h>
#define inf 0x3f3f3f3f
using namespace std;
const int maxn = 1e4 + 5;
int n,m;
int qry[105];
int head[maxn],idx;
bool vis[maxn],ans[105];
int dis[maxn],bel[maxn];
int siz[maxn],wei[maxn],ssiz,rt;
struct edge{int v,w,nxt;}e[maxn << 1];
bool cmp(int x,int y){return dis[x] < dis[y];}
void adde(int u,int v,int w)
{
    e[++idx] = edge{v,w,head[u]};
    head[u] = idx;
}
void dfs1(int u,int fa)
{//找重心
    siz[u] = 1,wei[u] = 0;
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (v == fa || vis[v])
            continue;
        dfs1(v,u);
        siz[u] += siz[v];
        wei[u] = max(wei[u],siz[v]);
    }
    wei[u] = max(wei[u],ssiz - siz[u]);//还有根到u的那一段
    if (wei[u] < wei[rt])
        rt = u;
}
void dfs2(vector<int>&a,int u,int dist,int fa,int root)
{//找出子树内的点和它们所属的子树和离根节点的距离
    a.push_back(u);
    dis[u] = dist,bel[u] = root;
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (v != fa && !vis[v])
            dfs2(a,v,dist + e[i].w,u,root);
    }
}
void calc(int u)//计算
{
    vector<int>a = {u};
    dis[u] = 0,bel[u] = u;
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (!vis[v])
            dfs2(a,v,e[i].w,0,v);
    }
    sort(a.begin(),a.end(),cmp);
    for (int i = 1; i <= m; i++)
    {
        auto l = a.begin(),r = a.end() - 1;
        while (l != r && !ans[i])
        {
            if (dis[*l] + dis[*r] > qry[i])
                r--;
            else if (dis[*l] + dis[*r] < qry[i])
                l++;
            else if (bel[*l] == bel[*r])
            {
                if (dis[*r] == dis[*(r - 1)])
                    r--;
                else
                    l++;
            }
            else
                ans[i] = 1;
        }
    }
}
void dfs(int u)//分治
{
    vis[u] = 1;
    calc(u);
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (vis[v])
            continue;
        wei[rt = 0] = inf;
        ssiz = siz[v];
        dfs1(v,0);
        dfs(rt);//以重心为根进行分治
    }
}
signed main()
{
    scanf("%d%d",&n,&m);
    for (int i = 1,u,v,w; i < n; i++)
    {
        scanf("%d%d%d",&u,&v,&w);
        adde(u,v,w);
        adde(v,u,w);
    }
    for (int i = 1; i <= m; i++)
    {
        scanf("%d",qry + i);
        if (!qry[i])//这里要特判 qry[i] = 0 的情况。
            ans[i] = 1;
    }
    wei[rt = 0] = inf;
    dfs1(1,0);
    dfs(rt);
    for (int i = 1; i <= m; i++)
        puts(ans[i] ? "AYE" : "NAY");
    return 0;
}

P5563 [Celeste-B] No More Running#

题意：给定一颗树，对于每个点 uu 求以 uu 为端点的路径长度在模 modmod 意义下的最大值是多少。

看到树上的路径问题，我们马上就想到了点分治。设当前的根是 rtrt，设 dis(u,v)dis(u,v) 表示 u,vu,v 之间的距离模 modmod。把当前分治区域内每个点 uu 到 rtrt 的距离统计出来。然后在统计答案的时候，我们发现，我们统计的每个距离都不会超过 modmod，这样子，两条路径加起来最多只会超过 modmod 一次。那么我们将超过 modmod 和不超过 modmod 分开讨论。把当前分治区域内每个点 uu 到 rtrt 的距离都插入一个 multiset 中，统计答案时，对于不超过 modmod 的情况，在 multiset 里二分找到最后一个小于 mod−disumod - dis_u 的元素；对于超过的，直接取最大的就行。

code:

CPP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include<bits/extc++.h>
#define int long long
#define max(x,y) ((x) > (y) ? (x) : (y))
#define min(x,y) ((x) < (y) ? (x) : (y))
#define inf 0x3f3f3f3f3f3f3f3f
const int maxn = 1e5 + 5;
int n,mod;
bool vis[maxn];
int head[maxn],idx;
int dis[maxn],ans[maxn];
int siz[maxn],wei[maxn],rt,ssiz;
std::multiset<int>st;
struct edge{int v,w,nxt;}e[maxn << 1];
void adde(int u,int v,int w)
{
    e[++idx] = edge{v,w,head[u]};
    head[u] = idx;
}
void dfs1(int u,int fa)
{
    siz[u] = 1,wei[u] = 0;
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (v == fa || vis[v])
            continue;
        dfs1(v,u);
        siz[u] += siz[v];
        wei[u] = max(wei[u],siz[v]);
    }
    wei[u] = max(wei[u],ssiz - siz[u]);
    if (wei[u] < wei[rt])
        rt = u;
}
void dfs2(int u,int fa)
{
    st.insert(dis[u]);
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v,w = e[i].w;
        if (v == fa || vis[v])
            continue;
        dis[v] = (dis[u] + w) % mod;
        dfs2(v,u);
    }
}
void set(int u,int fa,bool op)
{
    if (op)
        st.insert(dis[u]);
    else
        st.erase(st.find(dis[u]));
    for (int i = head[u]; i; i = e[i].nxt)
        if (int v = e[i].v; v != fa && !vis[v])
            set(v,u,op);
}
void dfs3(int u,int fa)
{
    ans[u] = max(ans[u],max(*(--st.lower_bound(mod - dis[u])) + dis[u],(dis[u] + *st.rbegin()) % mod));
    //这里就是在分讨两种情况。
    for (int i = head[u]; i; i = e[i].nxt)
        if (int v = e[i].v; v != fa && !vis[v])
            dfs3(v,u);
}
void dfs(int u)
{
    vis[u] = 1,dis[u] = 0;
    dfs2(u,0);
    ans[u] = max(ans[u],*st.rbegin());
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (vis[v])
            continue;
        //保证两个点一定不在同一个子树内
        set(v,u,0);//擦除 multiset 里的当前子树的点
        dfs3(v,u);
        set(v,u,1);//插入回去
    }
    st.clear();
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (vis[v])
            continue;
        wei[rt = 0] = inf;
        ssiz = siz[v];
        dfs1(v,u);
        dfs(rt);
    }
}
signed main()
{
    scanf("%lld%lld",&n,&mod);
    for (int i = 1,u,v,w; i < n; i++)
    {
        scanf("%lld%lld%lld",&u,&v,&w);
        adde(u,v,w);
        adde(v,u,w);
    }
    wei[rt = 0] = inf;
    ssiz = n;
    dfs1(1,0);
    dfs(rt);
    for (int i = 1; i <= n; i++)
        printf("%lld\n",ans[i]);
    return 0;
}

UVA12161 铁人比赛 Ironman Race in Treeland#

题意：有一颗树，树上的每条边有两个权值：长度和代价。一条路径的总代价是这条路径上的边的代价之和。求代价不超过 mm 的最长路径长度。

我们看到：不超过 mm，想到用一个单调的数据结构来维护。对于一条代价为 damagedamage 的路径，考虑在数据结构上二分出小于 m−damagem - damage 的最大的长度。既然如此，有结论：当 Di≤DjD_i \le D_j 且 Li≥LjL_i \ge L_j，肯定有 ii 比 jj 优，jj 就完蛋了。于是我们得维护一个 DD 和 LL 都单调的数据结构。std::map 是一个不错的选择。

code:

CPP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
#include<bits/extc++.h>
#define int long long
#define inf 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef pair<int,int> pii;
const int maxn = 2e5 + 5;
int n,k,ans;
bool vis[maxn];
int head[maxn],idx;
int siz[maxn],wei[maxn],ssiz,rt;
vector<pii>a;
map<int,int>mp;
struct edge{int v,d,w,nxt;}e[maxn << 1];
void read(int &x)
{
    x = 0; int f = 1;
    char ch = getchar();
    while (!isdigit(ch)){f = ch == '-' ? -1 : 1; ch = getchar();}
    while (isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}
    x *= f;
}
void adde(int u,int v,int d,int w)
{
    e[++idx] = edge{v,d,w,head[u]};
    head[u] = idx;
}
void dfs1(int u,int fa)
{
    siz[u] = 1,wei[u] = 0;
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (v == fa || vis[v])
            continue;
        dfs1(v,u);
        siz[u] += siz[v];
        wei[u] = max(wei[u],siz[v]);
    }
    wei[u] = max(wei[u],ssiz - siz[u]);
    if (wei[u] < wei[rt])
        rt = u;
}
void dfs2(int u,pii dis,int fa)
{
    a.push_back(dis);//把每个点到当前根的距离统计出来
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v,d = e[i].d,w = e[i].w;
        if (v == fa || vis[v])
            continue;
        dfs2(v,{dis.first + d,dis.second + w},u);
    }
}
void upd(int x,int y)
{
    auto p = mp.upper_bound(x);
    if (p == mp.begin() || (--p)->second < y)
    {
        mp[x] = y;
        p = mp.upper_bound(x);
        while (p != mp.end() && p->second <= y)
            mp.erase(p++);//对于那些不优的扔出去
    }
}
void calc(int u)
{
    mp.clear();
    mp[0] = 0;
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (vis[v])
            continue;
        a.clear();
        dfs2(v,{e[i].d,e[i].w},u);
        for (auto &[d,w] : a)
        {
            auto p = mp.upper_bound(k - d);//二分到最长的代价小于 k - d 的路径
            if (p != mp.begin())
                ans = max(ans,w + (--p)->second);
        }
        for (auto &[d,w] : a)
            upd(d,w);
    }
}
void dfs(int u)
{
    vis[u] = 1;
    calc(u);
    for (int i = head[u]; i; i = e[i].nxt)
    {
        int v = e[i].v;
        if (vis[v])
            continue;
        wei[rt = 0] = inf;
        ssiz = siz[v];
        dfs1(v,u);
        dfs(rt);
    }
}
void solve()
{
    read(n),read(k);
    fill(vis + 1,vis + n + 1,0);
    fill(head + 1,head + n + 1,0);
    ans = idx = 0;
    for (int i = 1,u,v,w,d; i < n; i++)
    {
        read(u),read(v),read(d),read(w);
        adde(u,v,d,w);
        adde(v,u,d,w);
    }
    wei[rt = 0] = inf;
    ssiz = n;
    dfs1(1,0);
    dfs(rt);
}
signed main()
{
    int t;
    read(t);
    for (int i = 1; i <= t; i++)
    {
        solve();
        printf("Case %lld: %lld\n",i,ans);
    }
    return 0;
}

P6329 【模板】点分树 | 震波#

看到题目，首先就想到对于每个查询都跑一边点分治。但是这样下来，时间肯定吃不消。这时候，我们就要引入点分树。

先来讲讲点分树是啥。我们先掏一颗树：

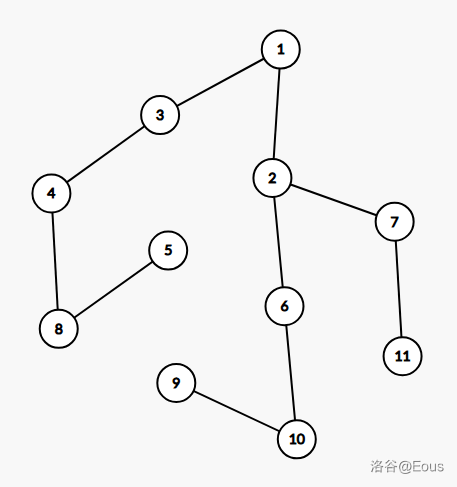
那么点分树就是当前分治中心到下一层分治中心连边，就像这样：

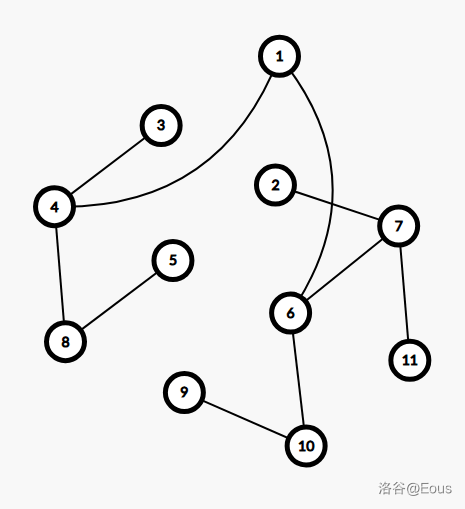
很显然和原树并没有什么关系。父子关系变得乱糟糟的。

但是，我们发现，点分树的树高只有 log⁡2n\log_2 n，简直就是暴力福音。还有，点分树上的 lca⁡(u,v)\operatorname{lca}(u,v) 一定在原树 u→vu \to v 的路径上。我们可以通过把原树上 u→vu \to v 的路径在点分树上 lca⁡(u,v)\operatorname{lca}(u,v) 这个点这里分开来处理路径问题。

回到这题。我们考虑枚举 x,ux,u 在点分树上的 lca vv，那么我们要找的答案就是：

ans=∑dis(x,v)+dis(v,u)≤kau=∑dis(v,u)≤k−dis(x,v)auans = \sum\limits_{dis(x,v) + dis(v,u) \le k}a_u = \sum\limits_{dis(v,u) \le k - dis(x,v)}a_u

让我们想想有什么 uu 会有 lca⁡(u,x)=v\operatorname{lca}(u,x) = v，明显是 vv 的整个子树扣掉 xx 所在的子树。对于每个点 xx 建树状数组，下标为 ii 的位置维护 ∑dis(x,v)=i\sum\limits_{dis(x,v) = i}。每次查询一个区间和就行。这样我们就搞定了一个路径。

但是一整条路径是要两条路径拼起来的啊，剩下的那条路径来自被扣掉的 xx 所在的子树。再对每个点都开一个树状数组。下标为 ii 的位置维护 ∑dis(u,fax)=iau\sum\limits_{dis(u,fa_x) = i}a_u，其中 uu 在 xx 子树内。每次查询 [0,k−dis(x,v)][0,k - dis(x,v)] 的区间和就行了。

code:

CPP
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
#include<bits/extc++.h>
#define int long long
#define inf 0x3f3f3f3f3f3f3f3f
#define lowbit(x) ((x) & (-x))
using namespace std;
const int maxn = 1e5 + 5;
int n,m,a[maxn];
vector<int>g[maxn];
vector<int>tree[maxn][2];
void resize(int id,int siz){tree[id][0].resize(siz),tree[id][1].resize(siz);}
void upd(int i,int id,int op,int val)
{
    for (i++; i < tree[id][op].size(); i += lowbit(i))
        tree[id][op][i] += val;
}
int que(int i,int id,int op)
{
    int ret = 0;
    i = min(i + 1,(int)tree[id][op].size() - 1);
    for (; i; i -= lowbit(i))
        ret += tree[id][op][i];
    return ret;
}
namespace ctr
{
    int siz[maxn],son[maxn],dep[maxn],top[maxn],fa[maxn];
    void dfs1(int u,int pre)
    {
        fa[u] = pre,dep[u] = dep[pre] + 1,siz[u] = 1;
        for (auto v : g[u])
        {
            if (v == pre)
                continue;
            dfs1(v,u);
            siz[u] += siz[v];
            if (siz[v] > siz[son[u]])
                son[u] = v;
        }
    }
    void dfs2(int u,int tp)
    {
        top[u] = tp;
        if (!son[u])
            return ;
        dfs2(son[u],tp);
        for (auto v : g[u])
            if (v != fa[u] && v != son[u])
                dfs2(v,v);
    }
    int lca(int u,int v)
    {
        while (top[u] != top[v])
        {
            if (dep[top[u]] < dep[top[v]])
                swap(u,v);
            u = fa[top[u]];
        }
        return dep[u] < dep[v] ? u : v;
    }
    int dis(int u,int v){return dep[u] + dep[v] - (dep[lca(u,v)] << 1);}
}
namespace algo
{
    bool vis[maxn];
    int ssiz,_min,rt;
    int siz[maxn],fa[maxn];
    int dfs1(int u,int fa)
    {
        int ret = 1;
        for (auto v : g[u])
            if (v != fa && !vis[v])
                ret += dfs1(v,u);
        return ret;
    }
    void dfs2(int u,int fa)
    {
        // cerr << "114514\n";
        siz[u] = 1;
        int _max = 0;
        for (auto v : g[u])
        {
            if (v == fa || vis[v])
                continue;
            dfs2(v,u);
            siz[u] += siz[v];
            _max = max(_max,siz[v]);
        }
        _max = max(_max,ssiz - siz[u]);
        if (_max < _min)
        {
            _min = _max;
            rt = u;
        }
    }
    void dfs(int u)
    {
        resize(u,dfs1(u,0) + 2);
        vis[u] = 1;
        for (auto v : g[u])
        {
            if (vis[v])
                continue;
            _min = inf,rt = 0;
            ssiz = dfs1(v,0);
            dfs2(v,0);
            fa[rt] = u;
            dfs(rt);
        }
    }
}
void upd(int u,int val)
{
    for (int i = u; i; i = algo::fa[i])
        upd(ctr::dis(i,u),i,0,val);
    for (int i = u; algo::fa[i]; i = algo::fa[i])
        upd(ctr::dis(algo::fa[i],u),i,1,val);
}
int que(int u,int k)
{
    int ret = que(k,u,0);
    for (int i = u; algo::fa[i]; i = algo::fa[i])
    {
        int dis = ctr::dis(algo::fa[i],u);
        if (dis > k)
            continue;
        ret += que(k - dis,algo::fa[i],0) - que(k - dis,i,1);
    }
    return ret;
}
signed main()
{
    // freopen("P6329_1.in","r",stdin);
    // freopen("out2.txt","w",stdout);
    scanf("%lld%lld",&n,&m);
    for (int i = 1; i <= n; i++)
        scanf("%lld",a + i);
    for (int i = 1,u,v; i < n; i++)
    {
        scanf("%lld%lld",&u,&v);
        g[u].push_back(v),g[v].push_back(u);
    }
    ctr::dfs1(1,0),ctr::dfs2(1,1);
    algo::_min = inf;
    algo::rt = 0;
    algo::ssiz = n;
    algo::dfs2(1,0);
    algo::dfs(algo::rt);
    for (int i = 1; i <= n; i++)
        upd(i,a[i]);
    int ans = 0,op,x,y;
    while (m--)
    {
        scanf("%lld%lld%lld",&op,&x,&y);
        x ^= ans,y ^= ans;
        if (op == 0)
        {
            ans = que(x,y);
            printf("%lld\n",ans);
        }
        else
        {
            upd(x,y - a[x]);
            a[x] = y;
        }
    }
    return 0;
}

好题推荐#

P4149 [IOI 2011] Race
P2664 树上游戏
CF293E Close Vertices
P3714 [BJOI2017] 树的难题